Phase Estimation

Phase

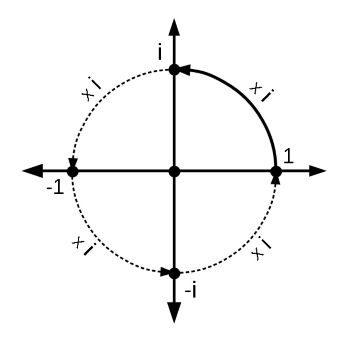
The word phase is used in many different ways in physics, but just think of it here as the angle that the hand of a clock makes to the 12 o'clock position. In quantum computing, one phase normally means one complete cycle which is 360 degrees or 2π radians. So if you imagine the hand on a clock turning through one complete revolution, its angular position θ would be changed by one complete phase, cycling around back to the value it started with. If θ is 0 at 12 o'clock, it would reach 2π when it gets back round to 12 o'clock and instantly reset to 0. The phase angle is always in the range 0 to 2π radians.

The equations of quantum mechanics include a phase factor e^-iθt which tracks the phase angle θ of a wave function as  it endlessly changes with time t. The phase factor always has unit value, but the proportions of its constituent real unit 1 and imaginary unit i change according to the cosine and sine of the phase angle. The math of quantum mechanics ensures that the unit value of the phase factor in the outer world is always preserved, whatever proportion of real and imaginary units the phase angle may point to, the inner subdivisions of  the unit 1 into its imaginary and negative parts slip below the radar of the uncertainty principle. The rate of change of phase in the wave function of a quantum system is proportional to the energy of the system.

There is a simplified guide to the cycling of phase and the role of the complex exponential e^-it in Chapter 4 of The Cosmic Computer.

The absolute instantaneous value of quantum phase is unmeasurable in the outer world where only the relative phase, the difference of phase angle between two systems is observable, and plays a vital role in interference effects and quantum computing with wavefunctions in superposition, as the relative phase controls whether superposed waves reinforce each other or cancel out.

The true absolute quantum phase is generally ignored and dismissed by physicists as meaningless because the uncertainty principle keeps it concealed from measurable effects, but an absolute global phase is always present in the quantum math and plays a background role in synchronizing all quantum systems even when they are separated.

Phase Estimation

Quantum phase estimation is one of the most important subroutines in quantum computing. It provides the means for Shor's algorithm to factor the very large non-prime number of an encryption key into its pair of smaller prime number components. It is the extreme difficulty of finding these factors with classical computers that ensures the security of the encryption.

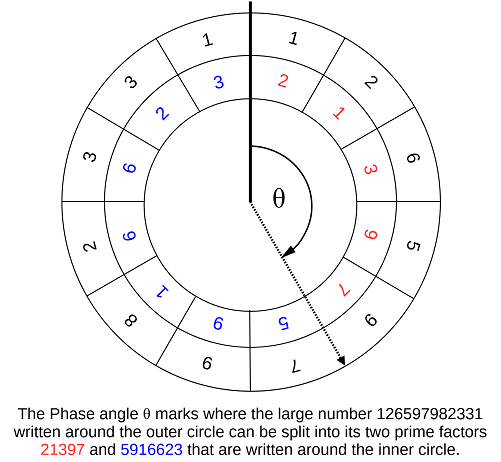
Imagine that the string of digits of the large composite number are written out in one loop around the circumference of a circle, like the time marks on a clock face. Finding the two prime factors would amount to finding the angle around the clock face where the two strings of digits join to be multiplied together.  The diagram below gives a rough idea of this for factoring the 12 digit number 126597982331 into its prime factors 21397 and 5916623, we need to determine the angle θ.

A controlled NOT or CNOT gate in a conventional computer consists of a control bit whose value decides whether or not the target bit must flip. Quantum computers use quantum CNOT gates, but strange things can happen if the control and target qubits are entangled, in fact the control qubit can end up changed itself by a phase shift while the target qubit remains unchanged! The target qubit is kept fixed by keeping it locked in an eigenstate, one of the only possible states it can take when measured in the outer world – it is partially anchored to the outer world. Because the target qubit cannot change its phase, any phase change induced by the control qubit can only produce a relative phase change in the control qubit. This is known as phase kickback.

Apart from qubits and quantum CNOT gates, the quantum phase estimation algorithm also requires quantum Hadamard gates that can transform a qubit between its discrete representation and its Fourier dual  representation as a superposition of many states – this transform just rotates a qubit. A Hadamard gate can also perform an inverse Fourier transform, rotating the qubit back to where it started. These quantum Fourier transforms are actually more efficient than the classical ones – quantum mechanical machinery is built for the job. In the phase estimation procedure, a Hadamard gate is used to transform the control qubit of the CNOT gate into superposition form before controlling the target qubit. There is an introduction to Fourier transforms and their fundamental role in information processing in Chapter 10 of The Cosmic Computer.

A single run of the phase estimation algorithm gives only a rough estimate of the phase, but by setting up a pointer register consisting of 1000 qubits in your quantum computer, you can repeat the phase kickback trick 1000 times, giving sequentially finer nudges to the phase of the set of qubits in the pointer register, each nudge being half the size of the previous one, thus quickly homing in on the true phase value. The final accuracy would be within one part in 2^1000, enough to determine the phase angle angle pointing to a prime number factor of a 300 digit decimal number, and crack any of our currently secure 256 digit encryption keys. In principle, if you want to factor larger numbers, you just need more qubits in your quantum computer.

The above is a simplified sketch of the phase estimation  procedure which also depends on several other special abilities of quantum computers, but it gives an idea of the extraordinary precision that Nature packs in its inner world of phase and particle spin – there is really nothing we can measure with anything like the accuracy of this 'estimation' procedure in our real outer world, and nowhere that information can be packed at such density.

Resources

Here are some links to more detailed accounts of phase estimation and Shor's algorithm that I have found useful. You can also play with quantum logic gates and see the effects they have on qubits.

IBM's guide to quantum phase estimation: https://quantum-computing.ibm.com/composer/docs/iqx/guide/quantum-phase-estimation

IBM's quantum computing guide to Shor's algorithm: https://quantum-computing.ibm.com/composer/docs/iqx/guide/shors-algorithm#shors-algorithm

Jonathan Hui on phase estimation: https://jonathan-hui.medium.com/qc-phase-estimation-in-shors-algorithm-acef265ebe50

Qiskit allow you to play with qubits and quantum gates as well as explaining the theory.

Qiskit on multiple qubits and entangled states: https://learn.qiskit.org/course/ch-gates/multiple-qubits-and-entangled-states

Qiskit on phase kickback: https://learn.qiskit.org/course/ch-gates/phase-kickback

Qiskit on quantum phase estimation: https://github.com/qiskit-community/qiskit-textbook/blob/main/content/ch-algorithms/quantum-phase-estimation.ipynb